| 本稿では、一流ランナーにおける競技距離とスピードの関係を探ります。
「フルマラソンのタイムを予測したい」、「400が専門だが800の可能性を知りたい」などと いう方は必見です。 本サイトの記事「世界記録、日本記録に見る競技距離とスピードの関係」で次のことを述べました。 横軸に距離の常用対数(※)を取り、縦軸にスピードをとると、1500mを境に2本の直線が表れる。 これはホモサピエンスとか日本人という抽象的なランナーの特性を表すものでした。 ならば、個人でも同様の傾向があるのではないかと考え、以下のようにデータを選択してグラフにしました。 ・長距離ランナーでは1500m以上の記録を使う。 ・短距離ランナーでは200m〜1500mの記録を使う。 まずご登場願うのは、次の方々です。 ウィルソン・キプケテル氏 800mの元世界記録保持者 ジェレミー・ウォリナー氏 400mの金メダリスト(アテネ) ハイレ・ゲブレセラシェ氏 マラソン元世界最高記録保持者 幸田 高明氏 2011年東京マラソン7位(日本人3位)旭化成株式会社 ※ある数の常用対数とは、10の何乗であるかを表す数です。 例えば100は10の2乗なので2、10000は10の4乗なので4、1500では3.176・・・という数になります。 エクセルのセル関数を使うと、例えば5000の常用対数は =LOG(5000) と打てば簡単に求まります。 この年になって LOG なんぞを見るハメになろうたぁ 思わなかったぜい、という御仁もおいででしょうが ‘ 陸上は理系 ’ と料簡なすって下さい。 |
||
| 1. | 一流ランナーにおける競技距離とスピードの関係
紺色の◆は実測タイムから導いた実測スピードです。 ピンクの直線は近似直線で、予測スピードの線です。 グラフを描くと、ビシッと直線に乗っているのが分かります。 |
|
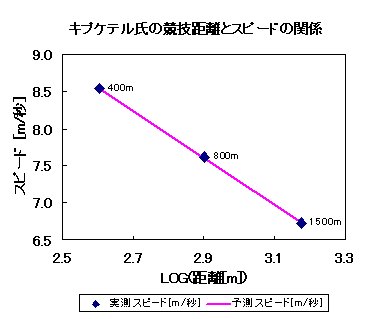 |
400m 46秒85 (1994年) 800m 1分45秒08 (1995年8月5〜13日) 1500m 3分42秒80 (1993年) ※1997年8月24日、世界記録 1分41秒11を樹 立しているが、400m、1500mの記録日に近い 1995年世界陸上のデータを採用。 |
|
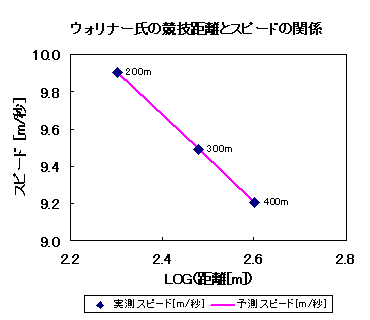 |
200m 20秒19 (2006/5/21) 300m 31秒61 (2008/6/12) 400m 43秒45 (2007/8/31) |
|
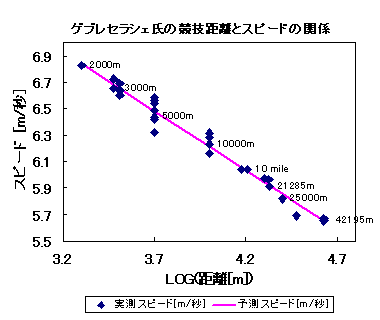 |
2,000m 4分52.86秒 (1998/02/15) 3,000m 7分30.72秒 (1996/02/04) 3,000m 7分26.15秒 (1998/01/25) 2 miles 8分07.46秒 (1995/05/28) 2 miles 8分01.08秒 (1997/05/31) 2 miles 8分04.69秒 (2003/02/21) 5000m 12分56.96秒 (1994/06/04) 5000m 12分44.39秒 (1995/08/16) 5000m 13分10.98秒 (1996/01/27) 5000m 12分59.04秒 (1997/02/20) 5000m 12分41.86秒 (1997/08/13) 5000m 12分39.36秒 (1998/06/13) 5000m 12分50.38秒 (1999/02/14) 10,000m 26分43.53秒 (1995/06/05) 10,000m 26分31.32秒 (1997/07/04) 10,000m 26分22.75秒 (1998/06/01) 10 km 27分02.00秒 (2002/12/11) 15 km 41分22.00秒 (2005/09/04) 10miles 44分24.00秒 (2005/09/04) 20 km 55分48.00秒 (2006/01/15) Half 58分55.00秒 (2006/01/15) 21,285m 60分00.00秒 (2007/06/27) 25 km 1時間11分37秒(2006/03/12) 30 km 1時間27分49秒(2009/09/20) Marathon 2時間4分26秒 (2007/09/30) Marathon 2時間3分59秒 (2008/09/28) |
|
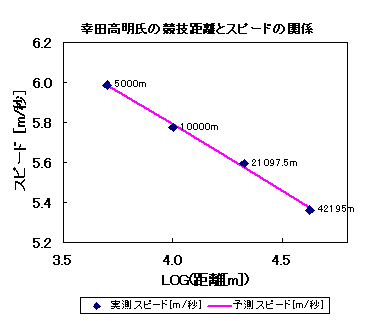 |
5000m 13分55秒19 (2008/07/09) 10000m 28分51秒23 (2008/07/16) ハーフマラソン 1時間02分52秒 (2008/03/16) マラソン 2時間11分08秒 (2011/02/27) |
|
| 2. | 近似直線の解釈
近似直線の式は、次のようになります。 スピード = スピード定数 − くたびれ係数 × LOG(距離[m]) ■スピード定数 は、LOG(距離[m])が0であるときのスピード です。 理屈では、距離1mを疾走するときのスピードです。実際にそのスピードで走られる訳ではありません。 スピードランナーと呼ばれる人達はこの値が大きくなっています。 ■くたびれ係数は、競技距離が延びるにつれてスピードを減少させる係数です。 くたびれ係数は小さいほど持久力が高く、大きいほど持久力が乏しい、といえます。 持久力が乏しいランナーでも、スピードにものを言わせ、くたびれる前にゴールする例が多々あります。 くたびれ係数が小さいランナーは、距離が長い競技で一線級に駆け上がる可能性があります。 ネーミングに適切を欠くきらいがありますが、持久力係数(*1)は別の定義で提唱されていますし、 くたばり係数では品位に難があり、疲れ果てて草に臥すという「くたびれ」係数で、まっいいかっ となった次第です。 ■ランナーは短距離用と長距離用とで合わせて2本のスピード近似直線を持っています。 たまたまNET上に、といっても2chなのでいささか難があるのですが、100m〜8000mの記録を載せた 方がいまして、もっともらしいデータなのでグラフにしてみました。(*2) 一人のランナーが2本のスピード近似直線を持っているんだ、という事例としてご覧下さい。 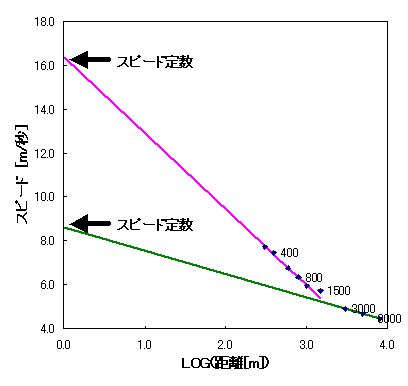 図2−1
ピンクと緑のスピード近似直線があるのが分かります。 ピンクの直線はスプリント直線、緑の直線はマラソン直線とでも言えば分かり易いでしょう。 前節の4氏のグラフは、キプケテル氏とウォリナー氏がスプリント直線、ゲブレセラシェ氏と 幸田氏がマラソン直線です。 ■意味深長なのが緑のマラソン直線です。 長距離選手はスピードと持久力を求めて鍛錬しますが、それをグラフで表現すれば、マラソン直線を 上に押し上げ、傾きを小さくして平らにする鍛錬です。 しかし、スピード練習について、NPO法人あっとランナーの鈴木彰さんはメルマガ「BEST RUN! Vol.555」で次のように述べています。 「スピード練習の設定タイムが上がっていくことではなく、スピード練習の効果として レースタイムが上がっていくことが重要なわけで、ここを間違うと、あれあれ?スピード 練習の出来は良いのにレースタイムが出てこないぞ?状態の「インターバル上手」に なってしまうこともあるよ〜」 これは、速すぎるスピード練習をやると、マラソン直線ではなくスプリント直線のトレーニングになって しまいますよ〜、ということではないでしょうか。 なかなか難しいことでしたが、このグラフを発見して何やら分かった気がします。 ■さて、スピード定数とくたびれ係数はランナー毎に異ります。 スピード定数とくたびれ係数をグラフの横軸と縦軸にとってプロットしてみると、ランナーの分布図 が出来るでしょう。 ネットにレース実績が載っているランナー諸氏にご登場願って、係数の分布図を描いてみましょう。 |
|
| 3. | 一流ランナー達のスピード定数とくたびれ係数の分布
(1) 長距離ランナーの分布 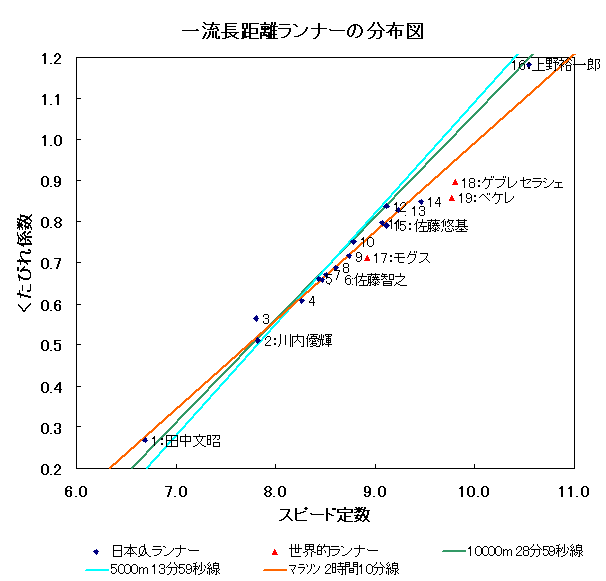 図3−1 ■ ランナーは左下から右上にかけて帯状に分布しています。 ・ 左上の分布がないのは、サンプルが一流ランナーばかりであるためです。 ・ 右下の分布がないのは、直感的には、不審ですが、ベケレ氏やゲブレセラシェ氏の位置を見れば 納得せざるを得ません。 ■ 直線は同一タイムになる点を結んだラインです。 ・ 例えばオレンジ色の線ですが、(スピード定数,くたびれ係数) の組がこの線上にあれば、 それがどこであろうとも、マラソンで2時間10分のタイムを期待できます。 この直線の傾きは競技距離によって決まります。タイムを短くすると下に平行移動し、長くすると 上に平行移動します。 ・ 箱根のスーパースターである上野氏は、驚いたことに、2時間10分線の上側にいます。 計算上の予言が外れて欲しいものです。 ・ そして、帯のもう一方の対局に川内氏と田中氏がいます。 5000、10000ではスーパースター達の後塵を拝する田中氏ですが、2009年春の結果で占うと、 マラソンでは勇躍、9分台前半になります。この予言は当たって欲しいものです。 まだ走っていますかね。 (2) スプリンターの分布 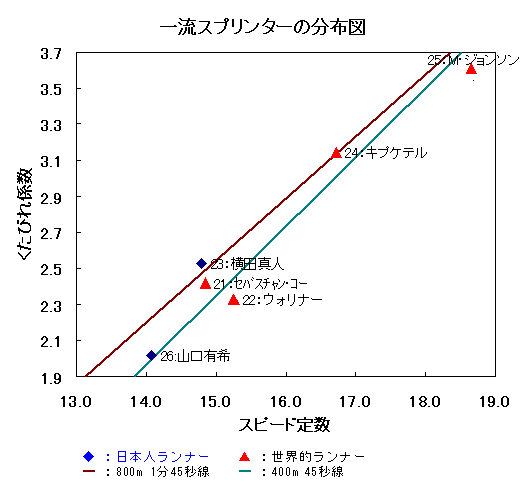 ■ ランナーは長距離と同様、左下から右上にかけて帯状に分布しています。 ・ スピード定数、くたびれ係数は共に、長距離ランナーより大きくなっています。 ■ 直線は同一タイムになる点を結んだラインです。 ・ 例えば茶色の線ですが、(スピード定数,くたびれ係数) の組がこの線上にあれば、 それがどこであろうとも、800mで1分45秒のタイムを期待できます。 ・ 400mが専門のウォリナー氏や山口有希氏は1分45秒線の下に位置しています。 各氏の800mの予測タイムは何と1分34秒、1分37秒になります。 こうなると突飛に過ぎますが、ひょっとするかも、と思ってしまいます。 (3) グラフに適用したデータの表 文末に添付します。 |
|
| 4. | まとめ
|
|
| ■個人記録について1500mを境として、競技距離の常用対数を横軸に取り、縦軸にスピードをとると、
直線上に並ぶ様子を見てきました。 予測性がありますので、未踏の種目に挑む際の目標になるでしょう。 ■タイムだけでは平板な情報しか掴めませんが、スピード定数とくたびれ係数を求めるとランナー の特性を読むことが出来ます。 夏期合宿の効果を計るための良い道具になるでしょう。 また、スピード定数とくたびれ係数の分布は、距離がまちまちである駅伝区間に選手を最適配置 するのに役立つでしょう。区間毎に目標タイム線を引いてみると意外な選手が脚光を浴びるかも 知れません。 |
||
| ※ | (*1)電気通信大の狩野豊准教授(生理学)が「 スピード持久力係数」を提唱されています。
(*2)記録の回数が多い競技は、自己ベストが高めに出るようです。図2−1の選手は1500が専門です。 |
|
| グラフに適用したデータの表 ※分散比は、直線への当てはめの善し悪しをはかる項目です。右隣のF値に較べて大きいほど当てはめがよいといえます。 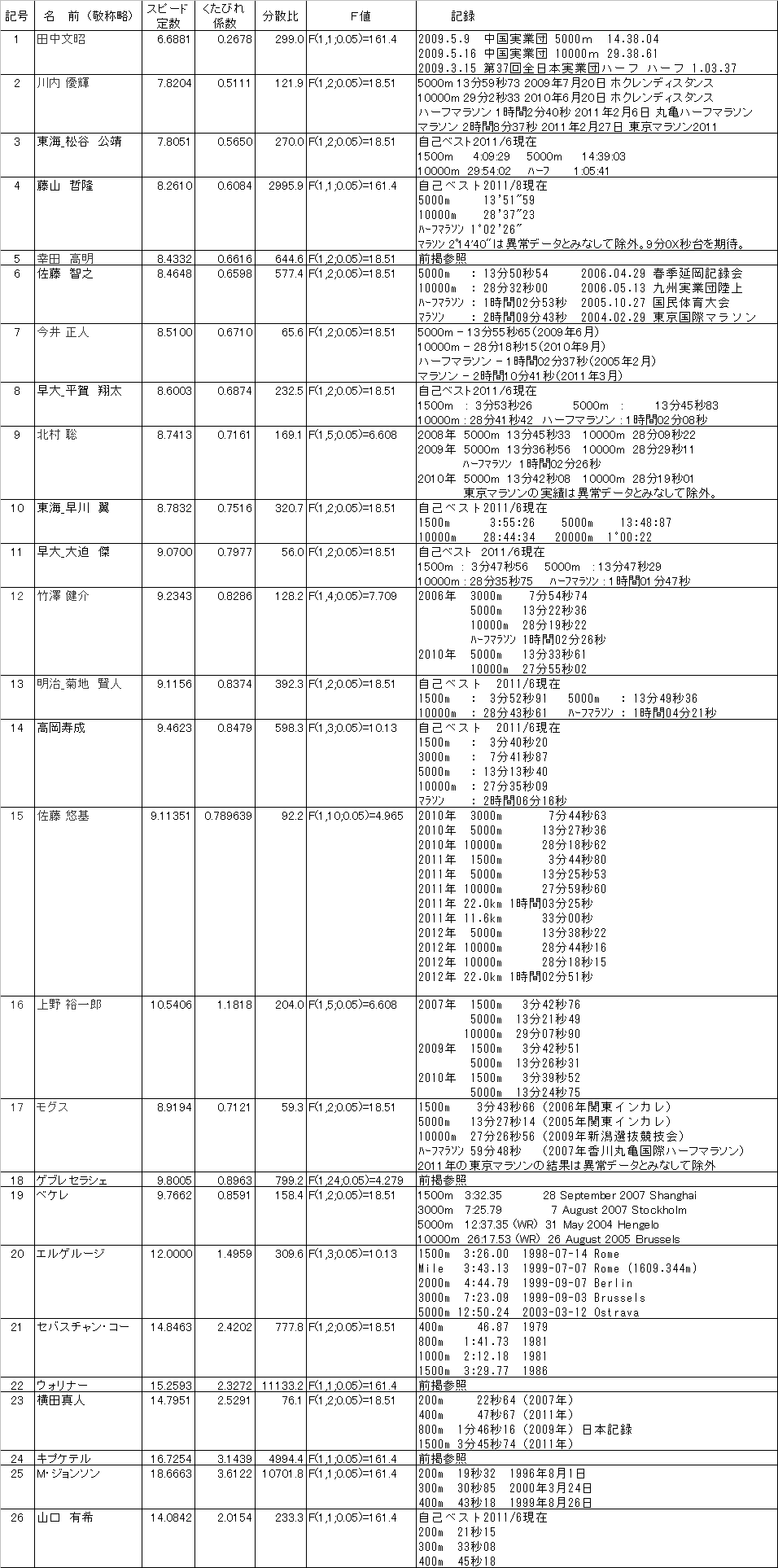 |